Yi-Ping Huang: Theory of emergent quantum matter
Quantum magnetism with large spin-orbit coupling
3d transition metal oxides provide various exotic phenomena of correlated electrons, i.e. Metal-insulator transition, superconductivity, etc. The competing effect between localized and itinerant physics made it an active research area in last fifty years. On the other hand, the discovery of topological insulator ignites the investigation of the new physics brings up by spin-orbit coupling. The interplay between correlation and spin-orbit coupling can provide the possibility to realize new phase of matter.
Topological order plays a unique role in the search of new phases of matter. Topological order is a quantum phase with long ranged entangled wave function which manifests the quantum nature of the phase. That is, it is impossible to construct such state from product states without gap closing.
Long-ranged entangled states are challenging to be realized in materials because: first, how long-ranged entangled wave functions emerge from a realistic microscopic model which is local? Second, if we obtain a particular long-ranged entangled wave function, how to have a positive diagnosis scheme to confirm the underlying quantum state is a long-ranged entangled state experimentally or numerically? It is thus necessary to find the sweet spot where experiments, theories, and numerical simulation meets to address such issue. Recent activities on the relation between symmetry and topological structure of the wave function provide a modern understanding of the long ranged entangled states. How to connect the new theoretical developments with realistic models to find better smoking gun evidence for the long ranged entangled states is an interesting and important question.
Ions with large spin-orbit coupling on pyrochlore lattice
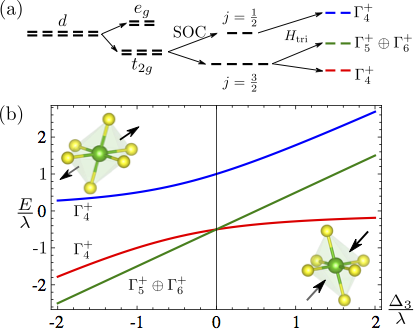
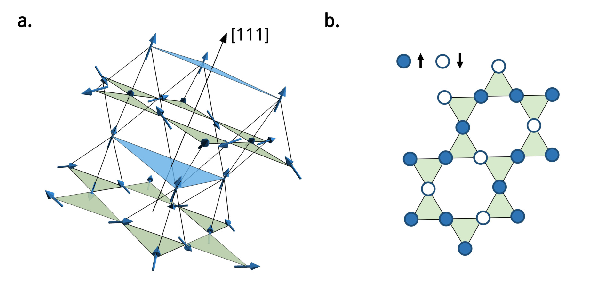
We study a family of materials of 5d or 4f ions on pyrochlore lattice. Considering both spin-orbit coupling and crystal field splitting, a type of Kramers doublets transform according to two distinct 1-dimensional irreducible representation under the \(D_{3d}\) site symmetry can be realized. We dub these doublets dipolar-octupolar(DO) doublets because the pseudo-spin operator formed by those doublets transform in a non-trivial way under symmetry operation. Such model has the potential to realize not only topological insulator but also quantum spin ices which are long ranged entangled quantum states in 3+1D at different limit. This work is published here.
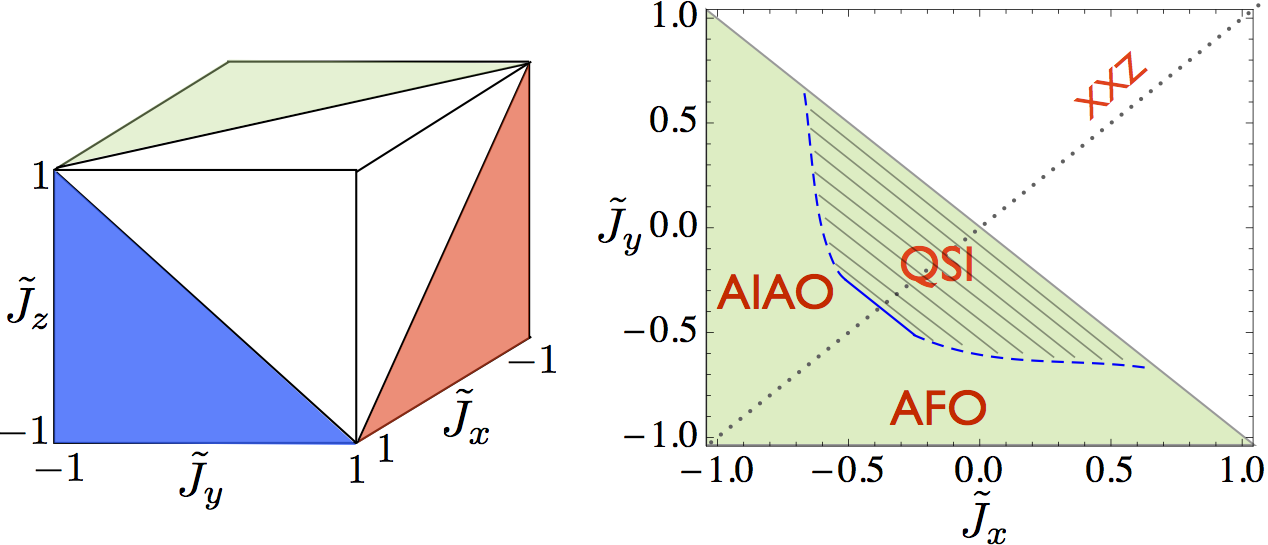
At the localized limit, we got a nearest-neighbor coupled XYZ exchange model on pyrochlore lattice. Because of the special transformation properties under site symmetry, the model is surprisingly simple. A large portion of the parameter space had no sign problem and can be studied with large scale quantum Monde Carlo. Besides, our model provides a "quasi-realistic" way to realize onsite \(Z_2\times Z_2\) symmetry for nearest-neighbor exchange model on pyrochlore lattice. The model could realize 3+1D symmetry enriched topological order with two distict topological order (dipolar quantum spin ice and octupolar quantum spin ice) protected by space group symmetry.
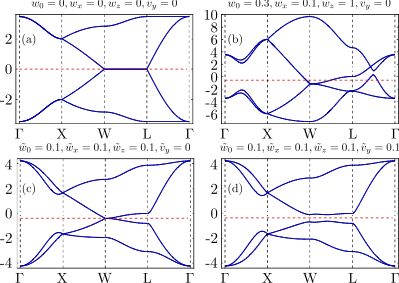
The non-trivial properties under site symmetry combined with the pyrochlore space group leads to two new low energy effective models at itenerent limit and localized limit. At itenerent limit, the model develop a "Dirac point like" band touching at W point till fourth nearest-neighbor hopping. By considering \(\mathbf{k}\cdot\mathbf{p}\) theory and construct the fourth nearest-neighbor hopping model, we prove the W point degneracy is not protected by space group. Once generic fourth nearest-neighbor hopping is included, the W point degeneracy will be removed. And leads to a strong topological insulator.

Updates
After our proposal, there are several interesting experiments about the dipolar-octupolar doublets. Related materials reveals various different kinds of physics including moment fragmentation, non-trivial all-in-all out order, and interesting disordered states. We list those articles here. Especially, recent work found disordered phases formed by octupolar components down to measurable temperature. It is exciting to have such experiments. The true nature of the disordered state is still not clear and worth further studies.
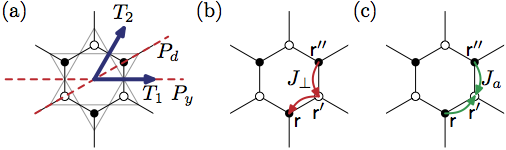
Theory of quantum Kagome ice and vison zero modes
Recently, significant advances in the theoretical understanding of the topological structure and the space group symmetry shed new lights on the possibility to detect global topological structure using symmetry defects. Several theoretical models demonstrate such behavior. However, very little attention has been paid to their physical consequences, and they have not been discussed in a simple, physically relevant model. In our work, we point out such idea provides striking numerical signals that can be measured using large scale unbiased quantum Monte Carlo simulation. We find the topological excitation transforms non-trivially under particular space group symmetry and global symmetry which leads to non-trivial local degeneracy, vison zero mode, that indicates the topological structure of the quantum states. This work is published here.
High energy Raman signal in \(Sr_2IrO_4\)
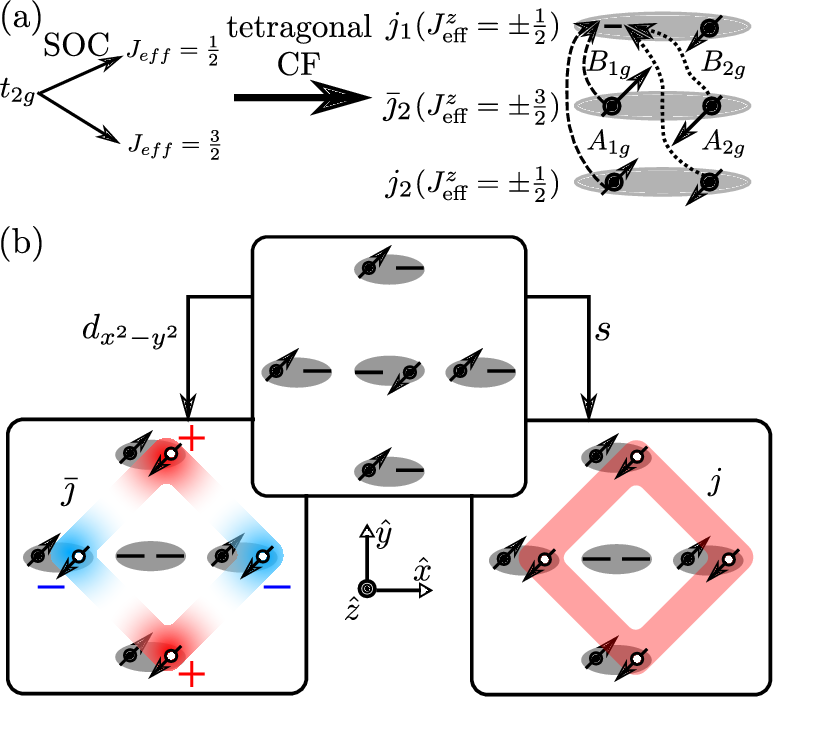
Spin-orbit interaction in \(Sr_2IrO_4\) leads to the realization of the \(J_{\mathrm{eff}} = 1/2\) state and also induces an insulating behavior. Local experiment group found two high-energy excitations of the d-shell multiplet at 690 meV and 680 meV with \(A_{1g}\) and \(B_{1g}\) symmetry respectively using large shift Raman spectroscopy. We give a simple theoretical model based on symmetry analysis explained the observed selection rules and suggest the corresponding possible microscopic mechanism. We show that both pseudospin-flip and non-pseudosin-flip dd electronic transitions are Raman active, but only the latter are observed. The experiments and analysis place significant new constraints on the possible electronic structure of \(Sr_2IrO_4\). This work is published here.
Building crystalline topological phases from lower-dimensional states
Topological phases protected by the geometrical symmetries of crystal lattices turn out to be surprisingly simple. They can be built from simpler lower-dimensional states, arranged in a crystalline pattern.
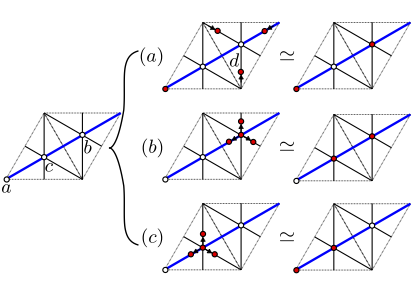
We study the classification of symmetry-protected topological (SPT) phases with crystalline symmetry (cSPT phases). Focusing on bosonic cSPT phases in two and three dimensions, we introduce a simple family of cSPT states, where the system is comprised of decoupled lower-dimensional building blocks that are themselves SPT states. We introduce a procedure to classify these block states, which surprisingly reproduces a classification of cSPT phases recently obtained by Thorngren and Else (arXiv:1612.00846) using very different methods, for all wallpaper and space groups. The explicit constructions underlying our results clarify the physical properties of the phases classified by Thorngren and Else, and expose additional structure in the classification. Moreover, the states we classify can be completely characterized by point-group SPT (pgSPT) invariants and related weak pgSPT invariants that we introduce. In many cases, the weak invariants can be visualized in terms of translation-symmetric stacking of lower-dimensional pgSPT states. We apply our classification to propose a Lieb-Shultz-Mattis–type constraint for two-dimensional spin systems with only crystalline symmetry, and establish this constraint by a dimensional reduction argument. Finally, the surprising matching with the Thorngren-Else classification leads us to conjecture that all SPT phases protected only by crystalline symmetry can be built from lower-dimensional blocks of invertible topological states. We argue that this conjecture holds if we make a certain physically reasonable but unproven assumption. This work is published here.
There is an old saying : 醉翁之意不在酒,在乎山水之間也。 In describe the following scenario. During the hiking, tasting the good wine in the mountain is not the goal. Instead the true purpose is to savour the beautiful view of the mountains.
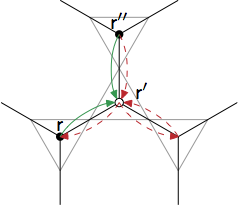
Tunneling-induced restoration of classical degeneracy in quantum kagome ice
Spin-orbit coupling reduces the symmetry of the system. It turns out we don't really understand the qualitative effects of the low symmetry. Especially, in a constrained Hilbert space, such as ice manifold, what is the effect of anisotropic quantum exchange process?
This problem is not only theoretically challenging but also numerically challenging. The low symmetry breaks a lot of nice properties and thus strong theorem such as LSM theorem is not useful for the analysis. In addition, the system with low symmetry usually does not have exact solvable points. Therefore, the analytic approach to study related problem is challenging.
From the numerical side, low symmetry also causes a problem for the tensor-network based algorithm. Without continuous symmetry such as U(1) and SU(2), the sparse format of the wave function is no longer valid and require higher bond dimension to study. Usual model with spin-orbit coupling will have the sign problem because of the nontrivial phase factor in the exchange process. It turns out we don't have much understanding from large-scale unbiased numerical methods for strong spin-orbit coupling systems.
One particular exception is the dipolar-octupolar doublets we discovered above. Analyzing the quantum Monte Carlo results with Prof. Ying-Jer Kao and his student Kai-Hsin Wu, we found the system stay in classical configuration down to very low temperature. Why the system acts so classical down to this low temperature is not clear. Using degenerate-perturbation theory, we found the effective theory at 6-th order has not only quantum tunneling term but also diagonal terms. Comparing with previous studies on pyrochlore lattice with U(1) symmetry, our system has only \(Z_2\) symmetry. In the U(1) case the comparable diagonal and quantum terms appear at the same lowest order only for spin with S>1/2. Thus, the low symmetry and constrained Hilbert space effectively increase the spin and make it more classical. This work can be found here