The advance in atomic, molecular, and optical physics allows us to explore emergent quantum phases of matter in different physical regimes. Various platforms ranging from cold atoms, ions, superconductor qubits, circuit QED provides different paths to study quantum many-body phenomena. In addition to the studies of hard condensed matter problems such as quantum simulation of Hubbard model and localization, the field has been extended to study gauge theories which play a fundamental role in our understanding of high-energy physics and constrained quantum systems such as frustrated magnetism.

In addition to the connections with various frontiers of studies, the synthetic quantum matter has advantages beyond conventional settings. For example, it provides a suitable framework to study fundamental questions in the dynamics of quantum many-body systems and quantum information sciences.

In the last several decades, studies of gapped quantum phases of matter have made significant advances on the classification of ground states and the characterization of low energy excitations. One of the key ingredients is the notion of many-body entanglement. The entanglement pattern gives us deep insights towards the understanding of many-body wave functions. It also becomes more and more evident that gauge theory plays an important role in describing the entanglement pattern.

However, how to extend the notion to the non-equilibrium setting is still an open question. To characterize a quantum many-body system, one needs to specify the Hilbert space, \(\mathcal{H}\), and the Hamiltonian, \( H \). In the study of quantum phases, one usually focus on ground state manifold. The fact that ground state manifold provides massive information of the system is because the Hamiltonian encode the physics of other excited states into the ground states. Similarly, excited states also contain partial information of the ground states. However, the third law of thermodynamics forbidden direct realization/probe of the system. It is therefore interesting to ask is it possible to understand the many-body ground states from experimentally accessible excited states?

How to prevent a quantum system from thermalization is an open and fundamentally important question. One approach to stop thermalization is to break ergodicity. In addition to integrability and localization by disorder, another possibility to break ergodicity is by local constraints. The lattice gauge theory(LGT) is a particular family of constrained systems where the local constraints are due to the gauge symmetry. It has also been observed that in certain one-dimensional LGT, ergodicity can be broken and lead to non-trivial dynamics. However, it is not clear whether such physics can be observed in a 2D interacting system. In this collaboration, we investigate this problem in a 2D LGT by applying a new numerical method. In LGT, a generic wave function can be understood as a superposition of different weighting of correlated "disorder configurations." Such interpretation naturally suggests the initial state controls the "disorder configuration" and could lead to ergodic or localization phenomena. The method overcomes the system size challenge and allows us to analyze the propagation of defects, the light cone structure and establish the localized and ergodic phase. This work is published here.

In equilibrium, phase transition happened when the free energy density develops non-analyticity at thermodynamic limit. For out of equilibrium quantum systems, the dynamics are governed by Schrodinger equation. The Loschmidt echo can be formally interpreted as partition function. The rate function of the Loschmidt echo thus plays a similar role to the free energy density. The dynamical quantum phase transition(DQPT) happens at the critical time when this quantity develops non-analyticity. The notion of phase transition is then generalized to a dynamical quantum system. The study of related phenomena is still at its infancy and most understanding is built from exact solvable models or low dimensional systems. It will be nice if we can find more examples that is beyond above mentioned situations.

The idea of quantum simulation has bee developed and applied on condensed matter related system for decades. Recently, the concept has been pushed forward to simulate gauge theories. One of the obstacles in quantum simulator is the local Hilbert space is usually of finite dimensional. Quantum Link Model(QLM) thus plays a special role that it provides the gauge structure using finite dimensional Hilbert space. Besides, recent quantum simulation experiments demonstrate the possibility of engineering gauge invariant Hamiltonian and coherent many-body real time evolution.

In this project, we explore the quench dynamics of gauge theories through the lens of dynamical quantum phase transitions. Using time-evolving block decimation (TEBD) and Lanczos-based exact diagonalization, we explore (1+1) d and (2+1) d QLMs. The advantage of using TEBD is it is almost exact in (1+1) d at short time. For (2+1) d, naive full spectrum ED will hit the wall of enumerating of states and it can only reach 4 by 4 (32 spin) system in a reasonable time. Using Lanczos-based method has two primary advantages. First, we perform exact time-evolution within the Krylov subspace where the information of the sparse many-body Hamiltonian is compacted in a dense effective matrix which is easy to solve. Second, the Krylov space is generated at run time which reduces the requirement of memory and allows us to go to larger system such as 4 by 6(48 spins) and 6 by 6(72 spins). Also, the Krylov space will stay in the same gauge sector automatically as the Hamiltonian is gauge invariant. This property helps us bypass the enumeration of gauge invariant states in a neat way. The problem thus becomes manageable.

Using the code I developed, we found DQPT in both (1+1) d and (2+1) d U(1) QLMs. We also found the corresponding order parameters and describe their physical meaning. This work can be found here.

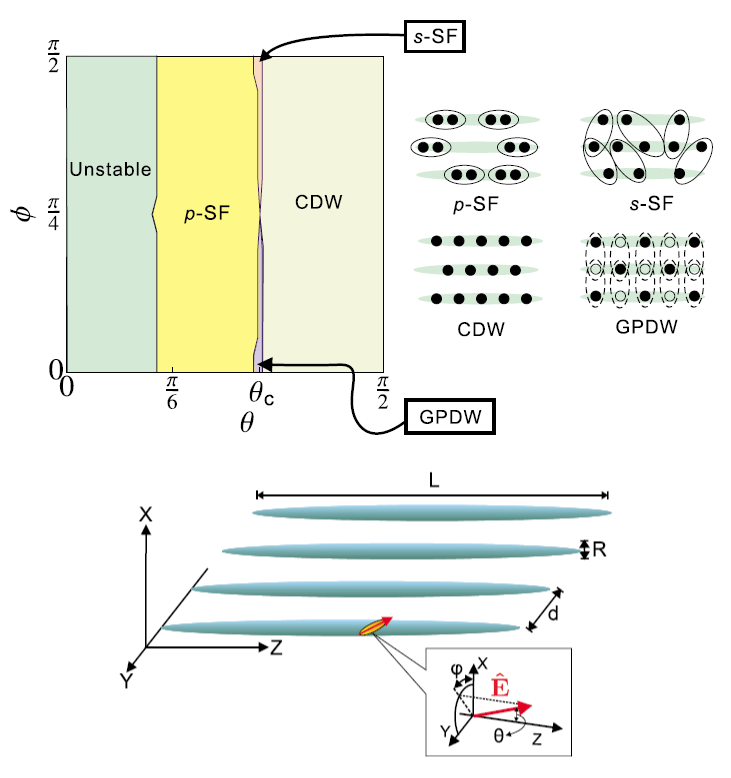
Dipolar gasses are unstable under head-to-tail configuration. To stabilize dipolar gasses, different geometric arrangements are proposed. Trapping dipolar gasses in 1D tubes is one possibility.

In this work, we generalize previous Luttinger liquid approach of two tubes into an arbitrary number of tubes lying in the same plane with arbitrary dipole orientation. Furthermore, we are able to map out the complete phase diagram for a different number of tubes under different dipole orientation. This work potentially can be realized in near future. This work is published here.